Large Language Masked Diffusion Models (LLaDA)

LLaDA: Diffusion Models that Finally Work for Text

Personal Introduction

Earlier this year, I was working on applying Diffusion and Consistency Models to the generation of embeddings in latent spaces in the NLP context, trying to replicate the success I achieved with time series imputation in my thesis. I wanted to bring that value into internal use cases at Avature where generative models could be very interesting.

I was inspired by research such as:

1. Latent Diffusion for Language Generation
2. TEncDM: Understanding the Properties of the Diffusion Model in the Space of Language Model Encodings
3. Continuous diffusion for categorical data

Despite the intensity and months of experimentation, the results were frustrating. Diffusion models for text have been historically more challenging than for images, and my experience confirmed this: generation quality was low and implementation unnecessarily complex. The approaches I tried did not achieve the desired coherence, which was frustrating given their success in other domains. Although I ended up with a consistency model (perhaps a future post will cover these models!) that gave some results, it was still unsatisfactory. For this reason, I abandoned this approach, at least temporarily.

Warning on complexity: Diffusion models for text have historically been much more challenging than for images. My personal experience confirms this: months of intense work with frustrating results.

The LLaDA Shift

However, a few weeks ago I came across the paper LLaDA (Large Language Diffusion Models). What struck me was its conceptual clarity and elegance. While I was struggling with continuous space and embeddings, LLaDA proposed a direct solution.

I realized that my approach of working with embeddings was a way of avoiding the discrete nature of text. LLaDA showed me it was possible to tackle the problem head-on by working with discrete tokens through masking. The difference was remarkable: I was able to make LLaDA work with relatively little implementation effort, compared to the weeks of debugging before.

In this post, I will share why this model works where others (including mine) failed, challenging the paradigm of autoregressive generation. And below I’ll share a link to the repository where I made a quick implementation of this.

Speculative note: I suspect that LLaDA’s approach (discrete diffusion with masking and parallel token prediction) is related to what Google DeepMind calls “Gemini Diffusion,” which describes block-based generation with iterative refinement. Reference: deepmind.google/models/gemini-diffusion.

Problems LLaDA Solves: The Attack on the AR Paradigm

LLaDA is not just another model; it is a direct challenge to autoregressive (AR) generation, the central dogma of modern LLMs. The authors of the paper question a fundamental assumption: the ability to generate intelligent text is not inherent to sequential order, but to the Transformer architecture, the amount of data, and the nature of generative training.

The Four Cracks of Autoregressive Generation

If we look closely, AR generation presents structural flaws that LLaDA seeks to overcome:

1. Prohibitive Computational Cost and Latency: Inefficiency is the most obvious. To generate a sequence of $N$ tokens, the model must perform $N$ passes through the network. That is, each time it predicts a new token, it must recompute the representation of the entire previous sequence. This makes decoding a slow and sequential process, limiting inference scalability.

2. Directional Reasoning Limitations: An AR model only learns to reason left-to-right. This directional restriction is a crucial obstacle in tasks that inherently require bidirectional context, as mentioned in the paper with text “reversal” tasks. The model cannot “look ahead” to ensure its current choice is coherent with the future.

3. Divergence and Error Accumulation (LeCun’s Problem): This, for me, is the most severe. As Yann LeCun has pointed out, if the model makes a mistake in predicting a token, that error propagates immediately: it contaminates the context for the next step. This leads to a chain of failures that grow exponentially. An AR model has no mechanism to correct an error once made. In contrast, diffusion-based models allow for iterative refinement.

   

4. Limited Learning Efficiency: Autoregressive training, seeing a sample always in the same way, quickly falls into overfitting. Diffusion models, by reusing the same sample under different levels of corruption or noise, show a greater ability to extract learning from the same amount of data. LLaDA scales better because it learns more efficiently.

---

Diffusion Generation: Why Previous Attempts Failed

To understand LLaDA’s breakthrough, we must recall what technical problems previous attempts to apply diffusion to text encountered.

The Fundamental Conflict: Discrete vs. Continuous

Diffusion models like DDPM were born and thrived in the image domain because they work with continuous latent spaces (pixel values). Text, however, is inherently discrete: each token is a fixed entity in a vocabulary.

Early approaches tried to force compatibility:

1. Diffusion in Embeddings (Continuous): Applying Gaussian diffusion to token embedding vectors (examples like TEncDM).

2. Discrete Adaptations: Trying to create discrete noise processes similar to Gaussian (example: Structured Denoising Diffusion Models).

Despite this, results were not as expected. And during 2023 and 2024, many saw diffusion models applied to text as a promise that never really took off.

My Personal Frustration: Invalid Regions

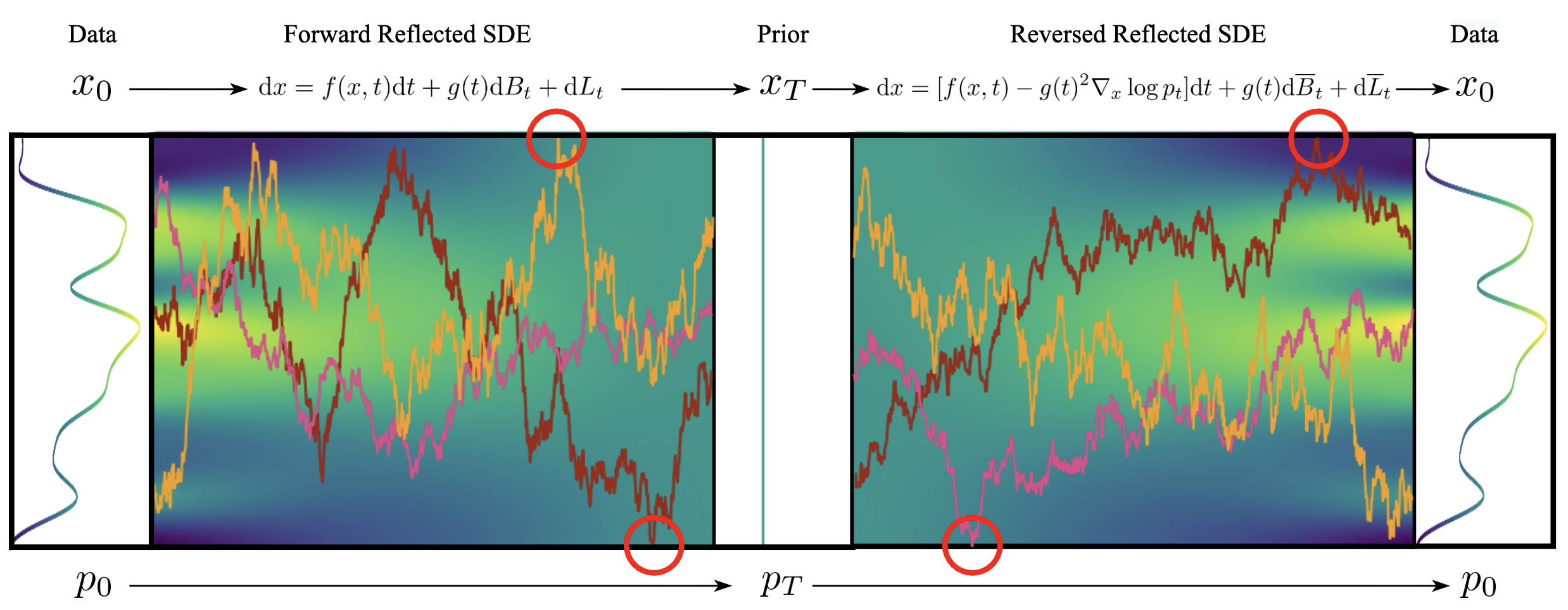
My months of experience ran straight into the problem described in Reflected Diffusion Models: the problem of invalid regions in latent space.

The problem of invalid regions: During denoising, errors can lead the model into regions of latent space that do not correspond to any valid token or sequence.

With images, an error means a blurry pixel. But with embeddings representing token sequences, denoising errors can lead you to vectors that:

1. Do not correspond to any real token in the vocabulary.
2. Represent semantically inconsistent combinations.
3. Are impossible to coherently map back to the discrete space.

In my implementation, this translated into generations that looked “almost correct” but produced nonsensical or incoherent sequences.

In the image above we can see how during a corruption process, and in another generation process, our samples can be erroneously guided into invalid space regions, marked with red circles.

Masked Diffusion Models

LLaDA’s solution is simple: abandon Gaussian noise and continuous space. It’s a deep conceptual shift:

Instead of starting from Gaussian noise, we start from fully masked tokens.

The analogy simplifies:

• Continuous Diffusion (DDPM): $\text{Gaussian noise} \rightarrow \text{Clean data}$
• Discrete Diffusion (LLaDA): $\text{Masked tokens} \rightarrow \text{Real text}$

The “denoising” process becomes progressive, iterative unmasking. This approach completely avoids the invalid regions problem because the model always operates in the discrete token space. This was the breakthrough that allowed LLaDA to succeed where all previous continuous attempts had failed.

How Does LLaDA Work?

Now that we understand why continuous approaches failed, we can dive into the brilliance of LLaDA. Its genius lies in its conceptual simplicity: it takes the successful intuition of diffusion and elegantly adapts it to the discrete world. LLaDA implements what we call discrete diffusion, keeping the iterative structure of DDPM but operating exclusively in the token space.

Masked Diffusion

Forward Process (Corruption)

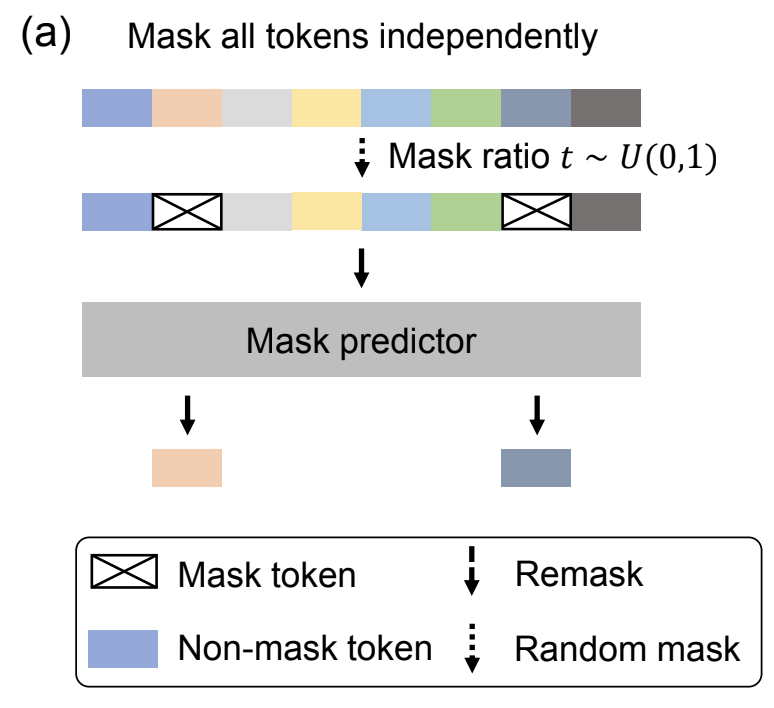
Instead of adding Gaussian noise as in traditional diffusion models, LLaDA applies stochastic masking, corrupting the original sequence $x_0$ by gradually turning tokens into masked tokens ([MASK]) over the diffusion steps.

Mathematically, for a data sequence $x_0 \sim p_{\text{data}}$, the corruption process is defined by a masking function:

\[\begin{equation} q(x_t|x_0) = \text{Mask}(x_0, t) \label{eq:forward_mask} \end{equation}\]

Masking depends on the corruption level $t \in (0,1]$ and during training is applied as follows:

1. Sampling: Sample the corruption level $t \sim \mathcal{U}(0,1]$ and a random mask $M \sim \mathcal{U}(0,1]$.

2. Application: The token $x_0^i$ becomes $\text{[MASK]}$ if $M^i < t$.

\[\begin{equation} x_t^i = \begin{cases} \text{[MASK]} & \text{if } M^i < t \\ x_0^i & \text{if } M^i \geq t \end{cases} \label{eq:masking_rule} \end{equation}\]

The parameter $t$ acts as the noise factor: $t \rightarrow 0$ means clean sequence; $t \rightarrow 1$ means almost fully masked sequence.

Loss Function

During training, the model learns to predict the original token $x_0$ given the masked inputs $x_t$. The loss function is a cross-entropy loss applied only to the masked positions, and it includes a smoothing factor $\frac{1}{t}$:

\[\begin{equation} \mathcal{L} = - \frac{1}{t \cdot L} \sum^L_{i=1} {\mathbf{1}[x_t^i = M] \log p_\theta(x^i_0|x_t)} \label{eq:loss} \end{equation}\]

This $\frac{1}{t}$ factor is key: it penalizes less when the sequence is almost fully masked ($t \approx 1$) than when only a few tokens remain to be refined ($t \approx 0$).

Reverse Process (Generation): Unmasking and Refinement

Generation is the inverse and gradual process in $T$ steps, starting from the fully masked state ($t=1$) to clean text ($t=0$).

Instead of predicting noise, the model $p_\theta$ directly predicts the probability distribution of the original tokens for all masked positions, and it does so simultaneously.

\[\begin{equation} \hat{x}_0 = \text{arg max } p_\theta(x_0 | x_t) \label{eq:reverse_predict} \end{equation}\]

This step of parallel generation is what fundamentally contrasts with the sequential nature of autoregressive decoding.

Re-masking Strategies

Once the network provides its predictions $\hat{x}_t$, we need to decide which tokens to “fix” and which to keep masked for refinement in the next step. Two strategies presented in the paper are:

1. Probabilistic Selection: Re-mask tokens with a decreasing probability at each step $t$, fixing those that are not masked again.
2. Confidence-based Masking: A smarter method is to re-mask probabilistically but prioritize refining those tokens where the model showed lower confidence (flatter probability distribution).

Generation Efficiency

Here lies a potential advantage over AR models: while they require $N$ passes through the network for $N$ tokens, LLaDA only requires $T$ passes. At scales where sequence length is very large ($N \gg T$), LLaDA’s generation speed is superior thanks to its parallel block prediction.

Though it’s worth noting that diffusion models also benefit from larger values of $T$ to better refine the generated sample.

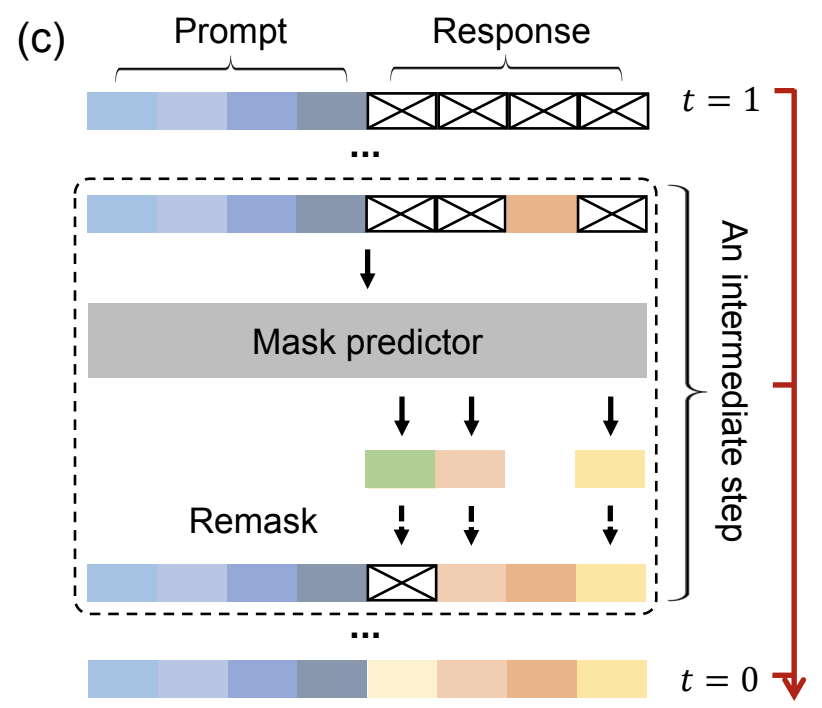
Conditional Generation (Fine-Tuning)

LLaDA’s structure allows an easy extension to conditional generation, necessary for tasks like in-context learning or instruction following.

We simply model the problem as generation conditioned on a prompt $ p_0 $, where we mask only the region intended for the LLM’s generated response:

\[\begin{equation} \hat{x}_0 = \text{arg max } p_\theta(x_0 | p_0, x_t) \label{eq:prompt} \end{equation}\]

Architecture and Constraints

Since LLaDA bases its generation on masks and requires attending to the entire sequence at once, it must be implemented with non-causal Transformers (similar to BERT), unlike autoregressive (AR) models.

This architecture brings a fundamental constraint: the impossibility of applying inference optimizations such as KV caching, a limitation that AR models can take advantage of.

LLaDA Results

The Key Advantage: Scalability and Data Efficiency

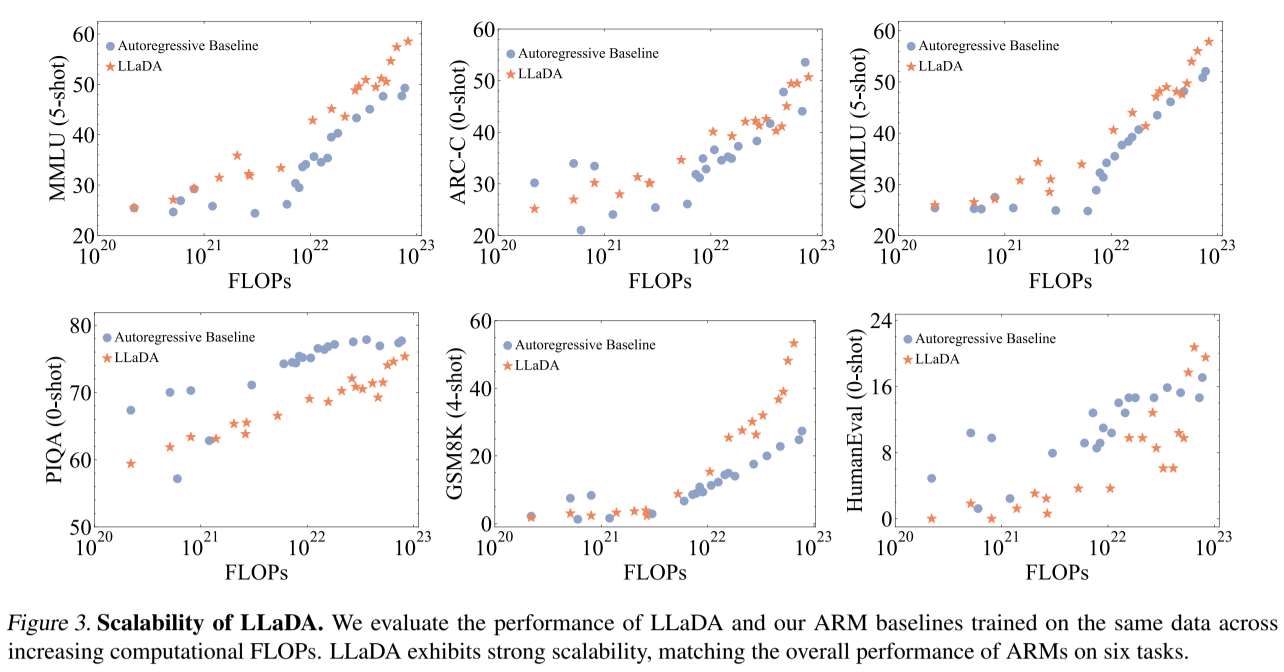
In the original paper, the authors built two basic Transformer models of 1B and 8B parameters to run their tests. While the paper provides a detailed analysis, the most revealing result in my opinion is related to scalability.

The figure shows that LLaDA’s scalability appears to surpass that of AR models as the amount of compute invested in training increases (i.e., more epochs given a fixed dataset).

This connects with what was described in the recent article Diffusion Language Models are Super Data Learners, where we can see the following results comparing diffusion models and autoregressive models:

As observed, for the same number of samples, diffusion models are able to continue extracting information from the data for more epochs, while AR models fall into overfitting. This is because diffusion reuses the same sample under different masking levels, offering different gradients and acting as a built-in regularization hack.

My Own Implementation

My previous experiences with diffusion were so frustrating that LLaDA’s approach motivated me to try it out and build a custom implementation as a personal proof of concept.

For this, I used the DistilBERT model (non-causal Transformer, 66M parameters), and the dataset: tinyStories (simple stories generated by GPT-3.5 and GPT-4).

The result, for such a small model and such quick training, was pretty good. Here’s a sample of how it works by generating a new story through the iterative unmasking process:

Personally, considering my previous experiences, I consider it a big success. If you want to see the code and experiment, here’s the GitHub repository.

---

Conclusions

Personally, I believe this work represents a turning point in how we approach text generation with diffusion models.

The most important lesson I take away is that conceptual simplicity beats technical complexity. While I got lost working with continuous embeddings and the invalid region problem, LLaDA works directly with discrete tokens, solving the problem and making the model more interpretable and easier to debug.

LLaDA is not a magic solution. The generation process requires $T$ sequential predictions. If this number $T$ is not significantly smaller than the length of the sequence to generate ($N$), efficiency advantages are questionable, especially since it cannot leverage AR models’ KV caching.

However, the difference is conceptual: by implementing LLaDA I learned that the most elegant solution is often the one that dares to question fundamental assumptions. I assumed continuous space was the only way; LLaDA showed me I was wrong, adapting diffusion to the natural mold of discrete text.

LLaDA is not just a technical breakthrough, it’s an invitation to challenge established paradigms in NLP. I encourage you to experiment and question other assumptions. The next big innovation might be waiting for someone brave enough to ask “why not?”.

---

References

Core Papers

• LLaDA: Large Language Diffusion Models – Original paper introducing masked diffusion for text
• Reflected Diffusion Models – Detailed analysis of the invalid regions problem in diffusion
• TEncDM: Understanding the Properties of the Diffusion Model in the Space of Language Model Encodings – Diffusion in continuous latent spaces
• Latent Diffusion for Language Generation – One of the earliest attempts to apply diffusion to text
• Continuous diffusion for categorical data – Adapting diffusion to discrete data
• Structured Denoising Diffusion Models in Discrete State-Spaces – Early proposal for discrete diffusion

Additional Resources

• Diffusion Language Models are Super Data Learners – Analysis on data efficiency
• Yann LeCun: Why LLMs are Doomed – Critique of autoregressive model limitations
• Gemini Diffusion – Description of Google DeepMind’s diffusion approach
• My LLaDA Implementation – Repository with example code