Los modelos de difusión (DDPM)

En este primer post de mi blog voy a intentar compartir todo lo que he aprendido sobre los modelos de difusión. Concretamente, vamos a enfocarnos en el artículo original que introdujo los Denosing Diffusion Probabilistic Models (DDPM), puedes encontrar la referencia al final de este post. Aparte de leer esta entrada, te animo a leer el artículo original también; es fascinante y puede ayudarte a entender mejor el modelo, especialmente si usas este blog y otros recursos que menciono más abajo, ¡que pueden ser incluso más útiles!

Si sólo buscas una introducción básica o un vistazo rápido a los modelos de difusión, este post puede que sea demasiado detallado para empezar. Aquí hablo de lo que me hubiera gustado saber cuando ya tenía una idea de cómo funcionaban estos modelos, pero quería entender a fondo su funcionamiento y matemáticas subyacentes. Si ese es tu caso, definitivamente revisa los recursos adicionales que comparto al final.

Resumen inicial

Los modelos de difusión son un tipo de modelo generativo. Esto significa que se entrena una red neuronal para aprender la distribución de unos datos, con el fin de que pueda crear nuevas instancias que encajen dentro de esa distribución. La clave de estos modelos radica en un cambio en su proceso de entrenamiento y generación, más que en la estructura del modelo en sí. Así que, básicamente, los DDPM son una forma diferente de entrenar y generar datos, pero no implican una nueva arquitectura de red.

Qué no es un modelo de difusión

Sin embargo, más que explicar qué es un modelo de difusión, me parece interesante comenzar definiendo lo que NO es.

Los DDPM no son:

• Una nueva arquitectura de modelo.
• Un nuevo tipo de capa neuronal.

Esto también es similar en el caso de las GANs (Generative Adversarial Networks), ya que el corazón de su cambio radica en el algoritmo de entrenamiento y se traduce en el uso de una función de pérdida adversarial para ajustar sus parámetros.

Ventajas y desventajas

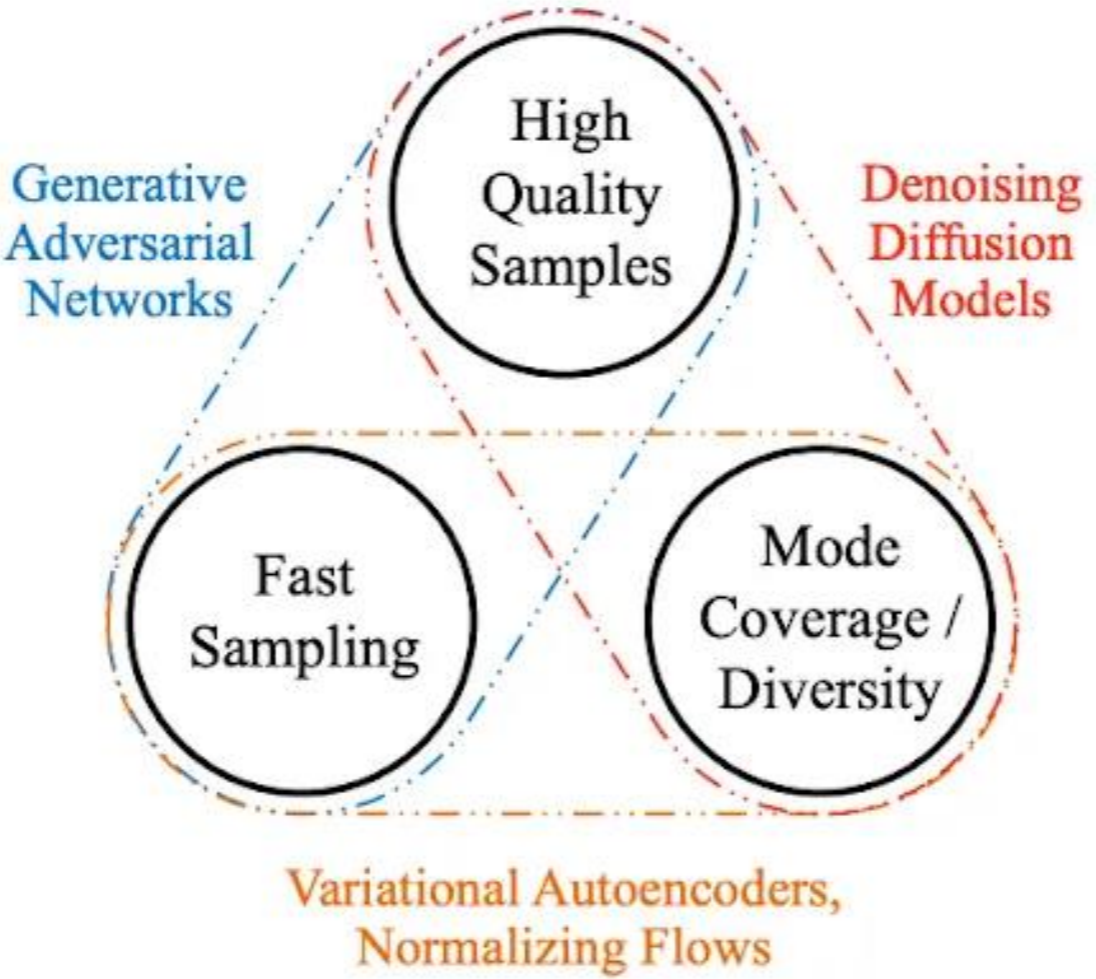Los 3 pilares de los modelos generativos y sus respectivos puntos fuertos

Básicamente, un modelo de difusion es un uno de los tres pilares de las técnicas de generación que hay hoy en día. Y se suele decir que cada pilar es bueno en 2 puntos, pero muy malo en el otro.

Concretamente, los modelos de difusión tienen las siguientes ventajas:

• Generan muestras nuevas de mucha calidad.
• Pueden aprender múltiples distribuciones a la vez.

Pero además, sobre las GANs, tienen la ventaja de:

• Convergencia mucho más estable al no tener dos modelos interactuando entre sí.
• No sufren del famoso problema del model collapse.

Sin embargo, sus desventaja principal es la lentitud de generación.

En el artículo original de los Denoising Diffusion Imputation Models (DDIM), se menciona que crear 50,000 imágenes de 32x32 pixeles usando GANs en una tarjeta Nvidia 2080 Ti lleva menos de un minuto. Sin embargo, con los modelos de difusión, estamos hablando de unas 1000 horas para la misma tarea.

Aunque por mucho tiempo se ha considerado a los modelos de difusión como uno de los pilares esenciales de los modelos generativos, últimamente esta regla de los 3 pilares se están volviendo menos clara. Gracias a mejoras como las introducidas por los DDIM, se está avanzando hacia superar las barreras de velocidad y abrir nuevos caminos para su uso práctico, rompiendo la desventaja en la velocidad de generación de los modelos de difusión.

Funcionamiento general

Un modelo de difusión básicamente toma unos datos originales y los va descomponiendo poco a poco, embarrándolos con ruido hasta que lo único que queda es una nube de ruido puro, o sea, datos que siguen una distribución normal estándar, que matemáticamente hablando se representa así: $\mathcal{N}(0, 1)$.

Este proceso de añadir ruido se realiza de manera gradual, siguiendo una serie de pasos predefinidos. Esto se puede describir usando lo que llamamos una cadena de Markov de $T$ pasos. Al comienzo, tienes una muestra inicial, a la que llamamos $x_0$, y al final del proceso, llegas a $x_t$, el punto donde los datos ya se han transformado completamente en ruido, cumpliendo que $x_t \sim \mathcal{N}(0, 1)$.

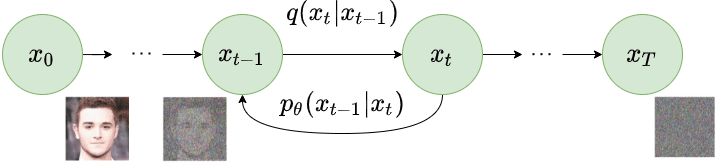Cadena de Markov. Avanzando por ella se va destruyendo la muestra, pero si se retrocede se va volviendo a su estado orignal

Para asegurarnos de que nuestros datos se transforman correctamente en ruido puro de la forma $\mathcal{N}(0, 1)$ a lo largo de la cadena de Markov, ajustamos cuidadosamente cuánto ruido añadimos en cada paso. Esto se hace mediante un parámetro llamado $\beta$. Este parámetro no es fijo; cambia progresivamente hasta que conseguimos que nuestros datos se conviertan completamente en ruido, alcanzando el estado $x_t \sim \mathcal{N}(0, 1)$. Por tanto, en cada paso de nuestra cadena tenemos un $\beta_t$ específico.

Podemos pensar en $\beta_t$ como si estuviera bajo el control de algo que llamamos el Scheduler, que vendría a ser como un objeto en Python encargado de manejar cómo evoluciona $\beta$ con el tiempo. Imagínatelo como una lista que va guardando cómo cambian los valores de $\beta_t$ para cada instante $t$. Y cuando necesitamos saber el valor de $\beta$ en un momento específico, simplemente le pedimos al Scheduler con algo así como scheduler.get_beta(t). Aunque hay varias estrategias que el Scheduler puede usar para definir estos valores, el enfoque original propuesto en el paper es utilizar un Scheduler lineal.

Pasamos de la distribución inicial a una máscara de ruido

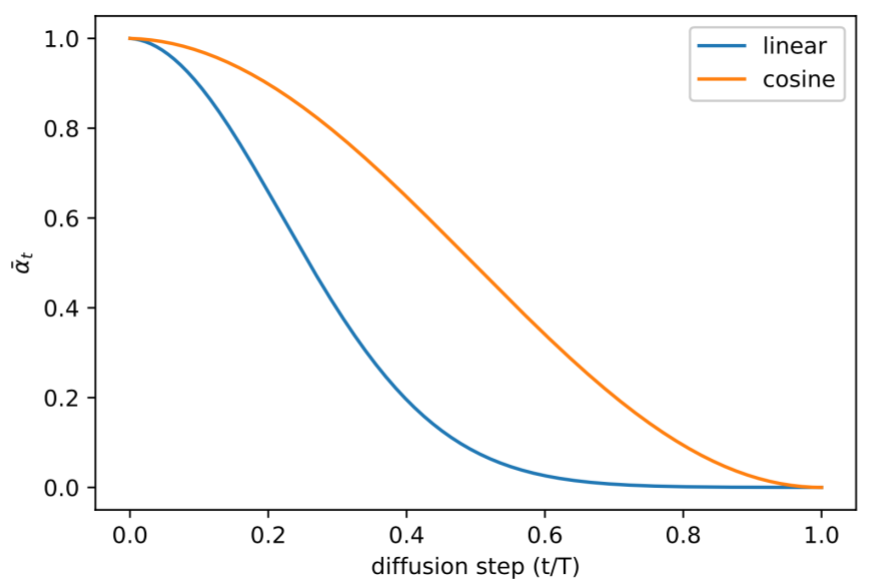El scheduler modificando la media de la distribución a lo largo de la cadena. En el primer caso se presentó el lineal, el del coseno fue presentado más tarde

Entonces, lo que buscamos hacer es entrenar un modelo que sea capaz de adivinar cuanto ruido hemos añadido en el momento actual. Si logramos predecir correctamente este ruido y lo eliminamos, deberíamos poder regresar al estado anterior de nuestros datos. Este proceso, hecho paso a paso de manera iterativa, nos permitiría, en teoría, usar nuestro modelo para prever las máscaras de ruido en cada etapa y, así, revertir completamente el proceso, pasando de $x_t$ a $x_0$.

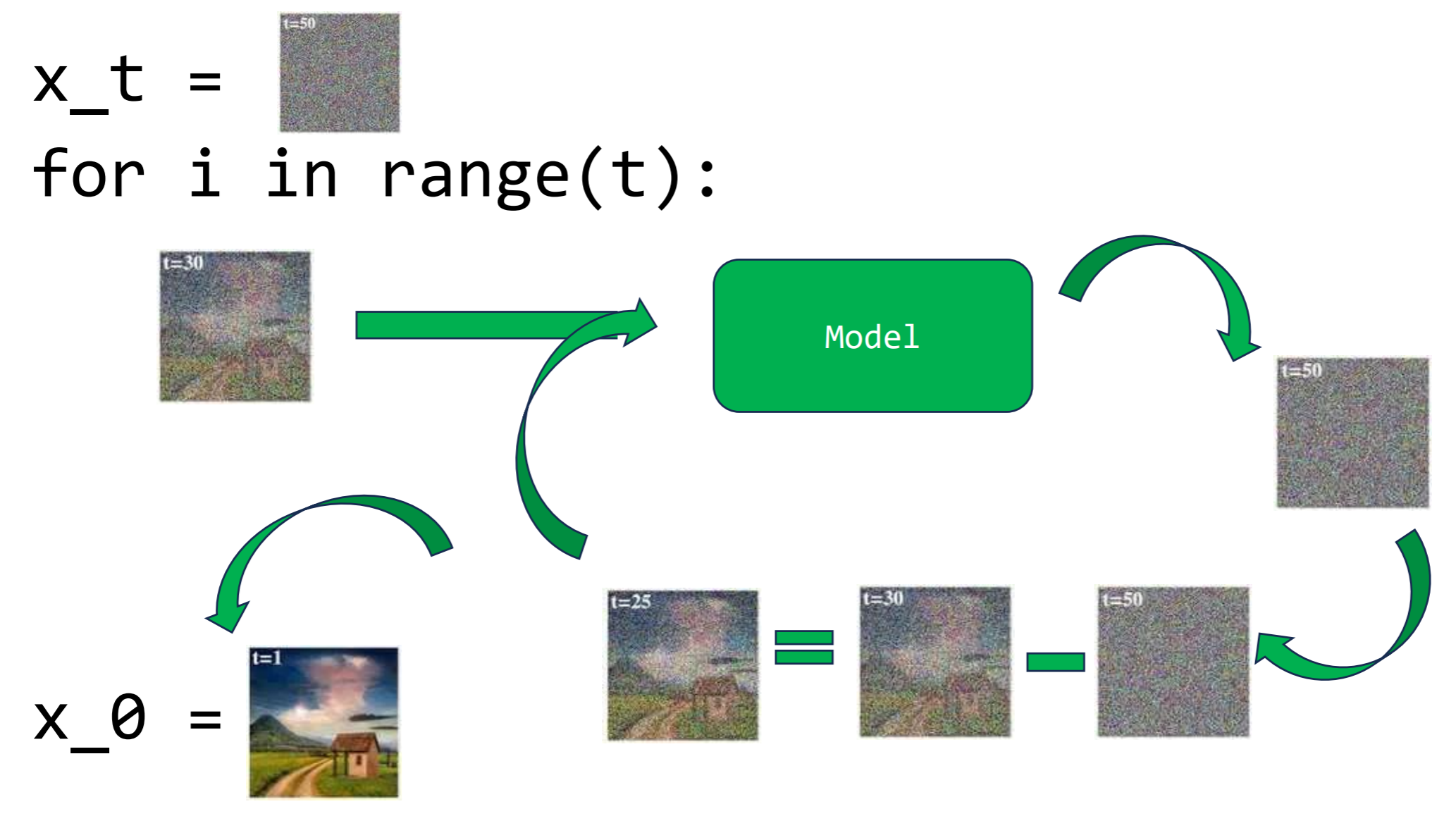Bucle para recorrer la cadena de Markov al revés y generar una muestra nueva. Se explicará con más detalle más adelante

Componentes principales de los modelos de difusión

Dicho esto, para entender bien los modelos de diffusión hay 5 elementos claves que tenemos que entender:

1. El Scheduler
2. El forward process $q(x_t$ l $x_{t-1})$
3. La posterior del forward process $q(x_{t-1}$ l $x_t, x_0)$
4. El bakward/reverse process $p_{\theta}(x_{t-1}$ l $x_t)$
5. La función de pérdidas

Scheduler

Como hemos visto anteriormente, la cantidad de ruido que añadimos en cada etapa de nuestra cadena de Markov varía; no es un valor fijo. Esto se diseña cuidadosamente para asegurar que, al final del proceso, terminemos con algo que se asemeje a $x_t \sim \mathcal{N}(0, 1)$. Si optáramos por añadir una cantidad constante de ruido en cada paso, la variabilidad de nuestra distribución se dispararía debido a la acumulación de este ruido, por lo que es crucial ajustar la intensidad del ruido que añadimos gradualmente. Aquí es donde entra en juego el Scheduler y el famoso $\beta_t$, que determina cuánto ruido añadir en cada paso.

En esencia, al inicio de cada paso generamos un nuevo conjunto de ruido de acuerdo a $\epsilon \sim \mathcal{N}(0, 1)$, y ajustamos su intensidad usando $\beta_t$. Profundizaremos más en este proceso más adelante, pero por ahora, es vital entender el papel del Scheduler, la función de $\beta_t$, y el hecho de que la cantidad de ruido que introducimos varía en cada paso.

Forward/Diffusion process $q(x_t|x_{t-1})$

Okay, hemos establecido que vamos a ir corrompiendo las muestras iniciales a lo largo de una cadena de Markov en la cual vamos a ir añadiendo ruido progresivamente, ¿pero cómo se hace esto?

El artículo nos ofrece una fórmula específica, la Fórmula \ref{eq:foward}, que nos guía en cómo avanzar de un estado $t-1$ al siguiente $t$. Esta fórmula es nuestra hoja de ruta para poder avanzar por la cadena.

\[\begin{equation} q(x_t|x_{t-1}) = \mathcal{N}(x_t; \underbrace{\sqrt{1-\beta_t}x_{t-1}}_{\mu}, \underbrace{\beta_t I}_{\sigma^2}) \label{eq:foward} \end{equation}\]

No te preocupes si la Fórmula \ref{eq:foward} te parece un poco enrevesada. Básicamente, lo que hace es aplicar una distribución normal con una media $\mu = \sqrt{1-\beta_t}x_{t-1}$ y una varianza $\sigma^2=\beta_t I$. De hecho, yo prefiero una versión más explícita de esta fórmula, que también presenta el artículo original. Vamos a definirla empezando por la base, con la fórmula de la distribución normal:

\[\begin{equation} \mathcal{N}(\mu, \sigma^2) = \mu + \sigma ·\epsilon \label{eq:normal} \end{equation}\] \[\epsilon \sim \mathcal{N}(0,1)\]

Con la definición de la distribución normal establecida en la Fórmula \ref{eq:normal}, podemos reformular la Fórmula \ref{eq:foward}. Esta nueva versión de la fórmula toma en cuenta los parámetros específicos de la distribución normal para aplicar el ruido a nuestras muestras a lo largo de la cadena de Markov.

\[\begin{equation} q(x_t|x_{t-1}) = \sqrt{1-\beta_t}x_{t-1} + \sqrt{\beta_t}\epsilon \label{eq:foward_explicit} \end{equation}\]

Con la Fórmula \ref{eq:foward_explicit}, para alcanzar cualquier punto $t$, solo necesitamos aplicarla de manera iterativa desde $t=0$, tal y como se muestra a continuación:

\[\begin{equation} q(x_{1:T}|x_0):=\prod^T_{t=1}{q(x_t|x_{t-1})} \end{equation}\]

Efectivamente, seguir este método paso a paso no es nada práctico, especialmente considerando que durante el entrenamiento necesitamos evaluar nuestra red con diferentes valores de $t$. Tener que recorrer toda la cadena hasta llegar a cada paso específico supone un coste computacional enorme. Por este motivo es necesario modificar la fórmula para obtener una nueva que nos permita saltar directamente desde $x_0$ a $x_t$, sin tener que pasar por cada paso intermedio. Comencemos definiendo las siguientes nuevas variables para simplificar este proceso:

\[\begin{equation} \alpha_t = 1 - \beta_t \end{equation}\] \[\overline{\alpha_t} = \prod^t_{s=1}\alpha_t\]

Así, $\overline{\alpha_t}$ encapsula de alguna manera la acumulación de todas las $\beta$ anteriores en la cadena. Esto nos permite reformular la Fórmula \ref{eq:foward_explicit} de una manera más eficiente y directa, facilitando el salto desde $x_0$ hasta $x_t$:

\[\begin{equation} q(x_t|x_0) = \sqrt{\overline{\alpha_t}}x_0 + \sqrt{1-\overline{\alpha_t}}\epsilon \label{eq:foward_xoxt} \end{equation}\]

Con la Fórmula \ref{eq:foward_xoxt} a nuestra disposición, ahora tenemos un mecanismo eficiente para transformar cualquier muestra original $x_0$ en su versión $x_t$ corrompida, correspondiente al paso $t$ de la cadena de Markov, usando un único salto. Esto simplifica enormemente el proceso y hace que el concepto de “Forward process” sea más accesible. Así que, de ahora en adelante, cuando hablemos del proceso forward, nos estaremos refiriendo específicamente a $q(x_t$ l $x_0)$ según lo define la Fórmula \ref{eq:foward_xoxt}.

Posterior de forward process $q(x_{t-1}|x_t, x_0)$

Vale, ahora vamos a enfocarnos en lo verdaderamente crucial: el proceso inverso. Necesitamos descubrir cómo podemos revertir el proceso, es decir, cómo retroceder a través de la cadena de Markov para recuperar la muestra original partiendo de su estado corrupto.

\[\begin{equation} q(x_t|x_{t-1}, x_0) = \frac{\overbrace{q(x_{t-1}|x_{t}, x_0)}^{\text{posterior}}q(x_{t}|x_0)}{q(x_{t-1}| x_0)} \label{eq:posterior_bayes} \end{equation}\]

Para lograr este retroceso en la cadena de Markov, aplicando el teorema de Bayes (detalle que puedes encontrar ampliado en la Fórmula \ref{eq:posterior_bayes}), conseguimos derivar este “posterior”. Este nos define cómo obtener el paso previo en la cadena, condicionado por el paso actual y por la muestra original. La definición de este posterior es la siguiente:

\[\begin{equation} q(x_{t-1}|x_t, x_0) = \mathcal{N}(x_{t-1};\tilde{\mu}_t(x_t,x_0),\tilde{\beta}_tI) \label{eq:posterior} \end{equation}\] \[\begin{equation} \tilde{\mu}_t(x_t,x_0) := \frac{\sqrt{\overline{\alpha}_{t-1}}\beta_t}{1-\overline{\alpha}_t}x_0 + \frac{\sqrt{\alpha_{t}}(1-\overline{\alpha}_{t-1})}{1-\overline{\alpha}_t}x_t \label{eq:mu_tilde} \end{equation}\] \[\begin{equation} \tilde{\beta}_t:= \frac{1-\overline{\alpha}_{t-1}}{1-\overline{\alpha_t}}\beta_t \label{eq:beta_tilde} \end{equation}\]

Es cierto que depender de $x_0$ en las fórmulas, especialmente las Fórmulas \ref{eq:posterior} y \ref{eq:mu_tilde}, puede ser un tanto incómodo. Esta dependencia se vuelve aún más problemática más tarde durante la generación de nuevas muestras, ya que en ese momento no contamos con $x_0$ disponible. Sin embargo, hay un truco que podemos emplear para sortear este inconveniente. Si consideramos que $q(x_t$ l $x_0) = x_t$, podemos despejar la Fórmula \ref{eq:foward_xoxt} para eliminar $x_0$. Haciendo esto, derivamos la siguiente nueva fórmula:

\[\begin{equation} x_0 = \frac{1}{\sqrt{\overline{\alpha}_t}}(x_t - \frac{1-\alpha}{\sqrt{1-\overline{\alpha}_t}}\epsilon) \label{eq:x_0_despejado} \end{equation}\]

Y si aplicamos la Fórmula \ref{eq:x_0_despejado} a la Fórmula \ref{eq:mu_tilde} se nos queda lo siguiente:

\[\begin{equation} \tilde{\mu}(x_t,x_0) = \frac{1}{\sqrt{\alpha}}(x_t-\frac{\beta_t}{\sqrt{1-\overline{\alpha}}_t}\epsilon) \label{eq:mu_tilde_despejada} \end{equation}\]

Con esto ya tenemos casi todo hecho, tenemos que realizar una última limpieza en la Fórmula \ref{eq:posterior}, para ello vamos a hacer lo siguiente:

Para darle los toques finales a la Fórmula \ref{eq:posterior} y dejarla lista para su uso, vamos a retocarla un poco más con tres pasos clave:

1. Aplicar la Fórmula \ref{eq:normal} que define la normal
2. Aplicar la definición de $\tilde{\mu}(x_t,x_0)$ que hemos obtenido en la Fórmula \ref{eq:mu_tilde_despejada}
3. Realizar una pequeña sustitución para simplificar un poco más, ya que sabemos que $x_t = q(x_{t-1}$ l $x_t, x_0)$

Con estos ajustes, logramos refinar nuestra fórmula, haciéndola más accesible:

\[\begin{equation} x_{t-1} = \frac{1}{\sqrt{\alpha}}(x_t-\frac{\beta_t}{\sqrt{1-\overline{\alpha}}}\epsilon_t) + \sqrt{\beta_t}\epsilon \label{eq:posterior_clean} \end{equation}\]

on la Fórmula \ref{eq:posterior_clean} en mano, estamos preparados para retroceder por la cadena de Markov. Pero, hay un pequeño detalle importante que señalar: la distinción entre dos tipos de $\epsilon$, que he diferenciado como $\epsilon_t$ y simplemente $\epsilon$, para evitar confusiones. Entender el papel de cada uno es crucial:

1. $\epsilon$ representa el ruido que se introduce al aplicar la normal. Este es el ruido específico que se añade en un paso dado para ajustarse a la definición de la distribución normal que aplicamos al volver hacia atrás.

2. $\epsilon_t$ es el elemento crítico en este contexto. Representa la suma total del ruido aplicado a $x_0$ para transformarlo en $x_t$. Este concepto es fundamental porque encapsula todo el proceso de difusión, reflejando la acumulación de ruido a lo largo de los pasos hasta alcanzar el estado actual.

Backwards process $p_{\theta}(x_{t-1}|x_t)$

Ahora que entendemos cómo navegar por la cadena de Markov, tanto hacia adelante como hacia atrás, el objetivo principal se centra en capacitar a nuestro modelo para que realice este proceso inverso eficazmente. Lo que buscamos es que $p_{\theta}(x_{t-1}$ l $x_t)$ aprenda a imitar el proceso de $q(x_{t-1}$ l $x_t, x_0)$.

Inicialmente, la definición del proceso inverso se establece de la siguiente manera:

\[\begin{equation} p(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t),\Sigma_\theta(x_t, t)) \label{eq:backward_full} \end{equation}\]

Efectivamente, de manera análoga a la Fórmula \ref{eq:posterior}, nuestro objetivo es ser capaces de predecir la distribución de la muestra en el paso anterior. Esto implica que, idealmente, deberíamos contar con un modelo (o incluso dos diferentes) que pueda predecir tanto la media $\mu_\theta(x_t, t)$ como la varianza $\Sigma_\theta(x_t, t)$ de la distribución normal en cuestión. No obstante, los autores del artículo original descubrieron que omitir la predicción de $\Sigma_\theta(x_t, t)$ llevaba a resultados más eficientes. Dado que la varianza ya está determinada por el Scheduler, podemos prescindir de predecirla, lo cual simplifica el proceso (aunque investigaciones posteriores han encontrado ventajas en predecir $\Sigma_\theta(x_t, t)$). Con este ajuste, la formulación del proceso inverso se simplifica considerablemente:

\[\begin{equation} p(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \beta_t I) \label{eq:backward_mu} \end{equation}\]

Entonces, llegados a este punto la media que tenemos que predecir es la siguiente:

\[\begin{equation} \mu_\theta(x_t, t) = \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{\beta_t}{\sqrt{1 - \overline{\alpha_t}}}\epsilon_\theta(x_t, t)) \label{eq:mu_prediction} \end{equation}\]

Así es, en el fondo, el parámetro crucial a predecir se convierte en $\epsilon_\theta(x_t, t)$, el cual representa efectivamente el ruido que se ha ido acumulando durante toda la cadena hasta el punto $t$. Esto nos indica cómo se ha modificado la muestra original para llegar a este estado específico de este paso de la cadena. Al predecir correctamente este ruido, podemos ajustarlo para el paso actual con el factor $\frac{\beta_t}{\sqrt{1 - \overline{\alpha_t}}}$, permitiéndonos eliminarlo gradualmente y, por tanto, avanzar en sentido inverso a través de la cadena.

Integrando lo que hemos visto, si reconstruimos la Fórmula \ref{eq:backward_mu} con la información de la Fórmula \ref{eq:mu_prediction} y la definición de distribución normal de la Fórmula \ref{eq:normal}, y consideramos que $x_{t-1} = p(x_{t-1}$ l $x_t)$, llegamos a la ecuación definitiva que nos permite retroceder paso a paso a lo largo de la cadena de Markov. Este proceso nos muestra cómo, a través de la predicción precisa del ruido en cada etapa, podemos retroceder por el camino de la difusión para recuperar la muestra original desde su estado corrupto.

\[\begin{equation} x_{t-1} = \frac{1}{\sqrt{\alpha_t}}(x_t - \frac{\beta_t}{\sqrt{1 - \overline{\alpha_t}}}\epsilon_\theta(x_t, t)) + \sqrt{\beta_t}\epsilon \label{eq:backwards_final} \end{equation}\]

Una vez más, vuelve a aparecer dos $\epsilon$ distintos, los volvemos a definir:

1. $\epsilon$ es el ruido que se le aplica para cumplir la definición de la normal.
2. $\epsilon_\theta(x_t, t)$ es el valor de ruido predicho por el modelo para calcular la media. Este valor representa el ruido acumulado que ha sido aplicado hasta el punto $t$ en la cadena. Predecir este ruido con precisión es esencial para poder revertir el proceso de difusión, eliminando el ruido añadido y recuperando la muestra original a medida que retrocedemos a través de la cadena.

Definición alternativa con $q(x_{t-1}|x_t, \hat{x}_0)$

Aunque la Fórmula \ref{eq:backwards_final} es la que comúnmente se utiliza y la que más se comenta cuando hablamos de modelos de difusión, es posible que en algunas ocasiones te encuentres con que se aplica $ q(x_{t-1} $ l $ x_t, \hat{x}_0) $ para retroceder a lo largo de la cadena.

En realidad, \(q(x_{t-1}\) l \(x_t, \hat{x}_0)\) y \(p(x_{t-1}\) l \(x_t)\) funcionan de manera muy similar, siendo la principal diferencia que la primera no elimina explícitamente $x_0$ de la ecuación, como se hace en el proceso que ya hemos visto y que lleva de la Fórmula \ref{eq:posterior} a la Fórmula \ref{eq:posterior_clean}.

Si te encuentras con esta fórmula, no hay motivo para preocuparse demasiado. Lo único que se hace es generar $\hat{x}_0$, que básicamente implica estimar la muestra original $x_0$ basándose en el estado actual $x_t$ y el ruido acumulado hasta ese punto:

\[\begin{equation} \hat{x}_0 = \frac{1}{\sqrt{\overline{\alpha_t}}}(x_t - \sqrt{1-\overline{\alpha_t}}\epsilon_\theta(x_t, t)) \label{eq:x_pred} \end{equation}\]

Puedes aplicar esto o simplemente entender que realmente son las mismas fórmulas y continuar utilizando la Fórmula \ref{eq:backwards_final} con tranquilidad, el resultado final será el mismo.

Consideraciones importantes

La imporantancia de t

La necesidad de incluir el tiempo $t$ como parámetro en los modelos es crucial, tal como hemos observado a lo largo de este post sobre los modelos de difusión. La razón detrás de esto es que el ruido añadido en cada paso de la cadena de Markov no es uniforme, lo que significa que el modelo necesita saber en qué punto específico se encuentra para poder estimar adecuadamente el ruido correspondiente.

Dificultad en mantener $x_0 \in [-1, 1]$

Uno de los desafíos con los modelos de difusión es la dificultad de mantener los valores de las muestras dentro del rango de [-1, 1] a medida que se elimina el ruido para retroceder por la cadena. Hay varias estrategias para abordar esto, aunque no todas son igualmente efectivas. Una táctica común es limitar los valores máximos que pueden alcanzar las muestras, pero esto puede ser insuficiente. Otra opción es normalizar nuevamente las muestras, lo cual puede ser una solución más efectiva para este problema.

En el último paso no añadimos ruido

Es importante notar, como se indica en la Fórmula \ref{eq:backwards_final}, que aunque generalmente añadimos ruido para cumplir con las definiciones de las distribuciones normales al retroceder por la cadena, no añadimos ruido en el último paso, es decir, al pasar de $x_1$ a $x_0$. Esto es lógico, ya que el objetivo final es recuperar la muestra original tal cual era, sin introducir ninguna alteración adicional en este punto crítico del proceso.

Función de pérdidas

La clave para enseñar a nuestro modelo a navegar eficientemente a través de la cadena de Markov y retroceder de manera precisa radica en la función de pérdida que empleamos durante el entrenamiento. Idealmente, querríamos que esta función fuera la log-likehood de $p_\theta(x_0)$, lo cual implicaría recorrer toda la cadena para cada batch de entrenamiento, un proceso extremadamente costoso y prácticamente inviable, como bien señala el artículo definiéndolo como un proceso intractable.

Para sortear este obstáculo, nos apoyamos en el concepto del Variational Lower Bound, que siempre es al menos menor que la log-likehood. Al optimizar esta función, indirectamente estamos mejorando la log-likehood, ya que el Variational Lower Bound siempre se sitúa por debajo de esta última.

Esta relación se ilustra claramente con la siguiente imagen, donde se muestra que al optimizar esta función, de hecho, mejoramos la log-likehood. Este enfoque nos permite entrenar nuestro modelo de manera eficiente, enfocándonos en mejorar esta cota inferior con la confianza de que, al hacerlo, también estamos mejorando la log-likehood de nuestro modelo.

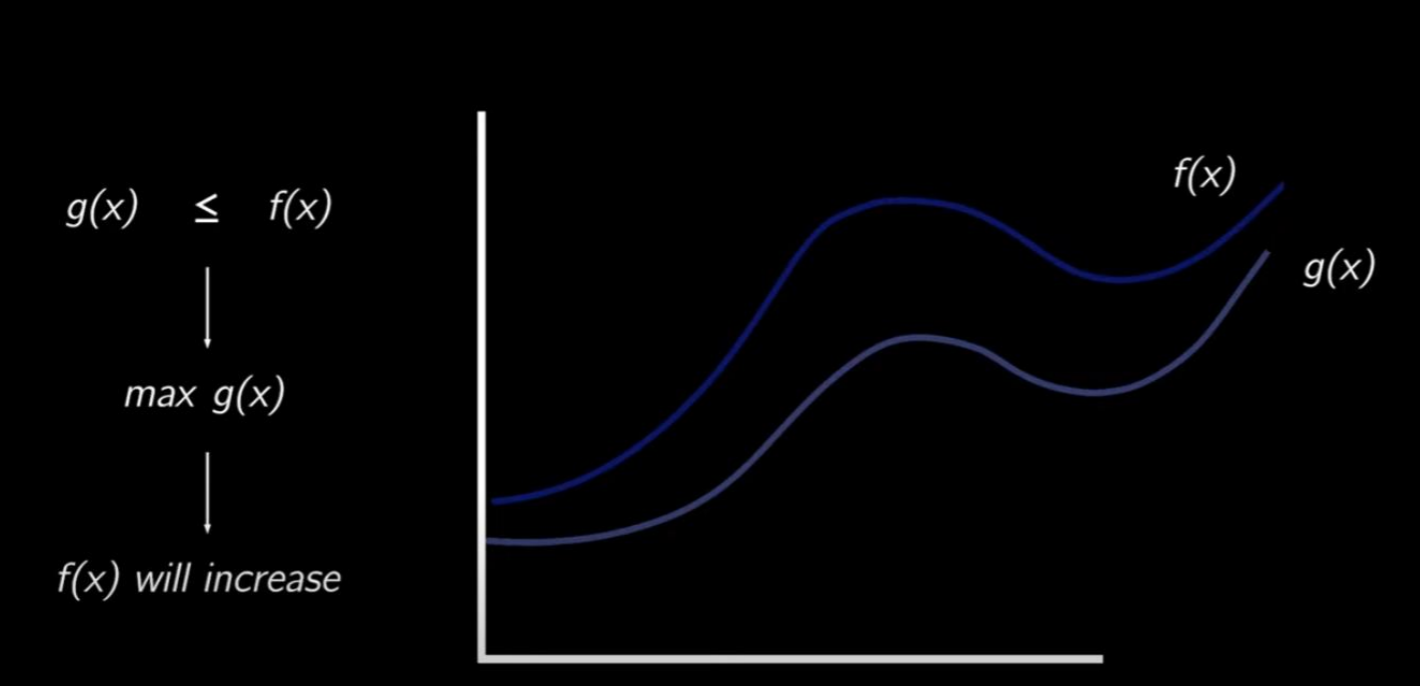Ejemplo de log-likehood y Variational Lower Bound. Está última siempre estará por debajo de log-likehood, y por lo tanto, mejorarla, acaba mejorando el log-likehood.

Básicamente, eso se define con la siguiente fórmula:

\[\begin{equation} \mathbb{E}[\underbrace{-\log{p_\theta(x_0)}}_{NLL}]\le\mathbb{E}_q[-\underbrace{\log p_\theta(x_0|x_1)}_{L_0} + \sum_{t>1}\underbrace{D_{KL}(q(x_{t-1}|x_t,x_0) || p_\theta(x_{t-1}|x_t))}_{L_{t-1}} +\underbrace{D_{KL}(q(x_T|x_0) || p(x_T))}_{L_T}] \label{eq:elbo} \end{equation}\]

La ecuación que tenemos ante nosotros puede parecer un reto a primera vista, pero vamos a desgranarla paso a paso para que resulte más comprensible:

• $NLL$: Es la negative log-likehood, se establece que siempre será igual o menor a lo que se encuentra a la derecha de la inecuación.

Apartir de aquí, el enfoque se centra en comparar qué tan similares son las distribuciones reales $q$ con las que nuestro modelo $p_\theta$ logra aprender. Esta comparación se hace a través de la divergencia KL. Así que:

• $L_0$: representa cómo se mide la negative log-likehood en el primer paso de la cadena.
• $L_{t-1}$: se refiere a la likehood de los pasos intermedios de la cadena.
• $L_{T}$: es sobre el último paso de la cadena. Aquí, básicamente, tenemos dos distribuciones de ruido $\sim\mathcal{N}(0,1)$, dictadas por el Scheduler, lo que nos permite simplificar y excluir esta parte de nuestra ecuación.

A pesar de todo, no teneis que tener miedo de esta pedazo de fórmula. Al final, lo que realmente importa para asegurar una buena aproximación en el proceso de reconstrucción es una estimación precisa de $\epsilon_\theta(x_t, t)$. Con esta idea en mente y haciendo una “limpieza” de la Fórmula \ref{eq:elbo}, se obtiene la siguiente simplificación:

\[\begin{equation} \mathcal{L} = \mathbb{E}_{t, x_o, \epsilon} [||\epsilon - \epsilon_\theta(x_t, t)||^2] \label{eq:loss} \end{equation}\]

Al final, lo que se nos queda como función de pérdidas es el MSE entre el error real y el predicho, algo sin duda mucho más manejable.

Algoritmos

Ahora que hemos interiorizado las bases matemáticas detrás de los modelos de difusión, es momento de echar un vistazo a los algoritmos que los hacen funcionar. A diferencia de las GANs, aquí encontraremos una distinción más marcada entre el algoritmo utilizado para el entrenamiento y el utilizado para la generación.

Entrenamiento

Algoritmo de entrenamiento

El funcionamiento es el siguiente:

1. Seleccionamos un batch de entrenamiento
2. Generamos aleatoriamente un valor de $t$ distinto para cada muestra
3. Generamos los $x_t$ según el $t$ que le haya tocado a cada uno y guardamos la matriz de ruido de cada una.
4. Usamos nuestro modelo para predecir la matriz de ruido en función de $x_t$ y $t$
5. Calculamos el mse entre el ruido real y el predicho y retropropagamos el error.

Generación

Algoritmo de generación de muestras

Es un poco diferente al anterior, pero básicamente lo que tenemos que hacer es lo siguiente:

1. Generar un batch con tantas matrices de ruido aleatorio como muestras queramos generar. Estas serán nuestras $x_t$
2. Realizar la predicción del ruido que tienen mediante el uso de nuestro modelo utilizando $x_t$ y $t$.
3. Reconstruir $x_{t-1}$ con el ruido predicho.
4. Repetir hasta haber recorrido toda la cadena.

De esta forma, apartir de un ruido aleatorio, nuestro modelo termina generando unas muestras totalmente nuevas.

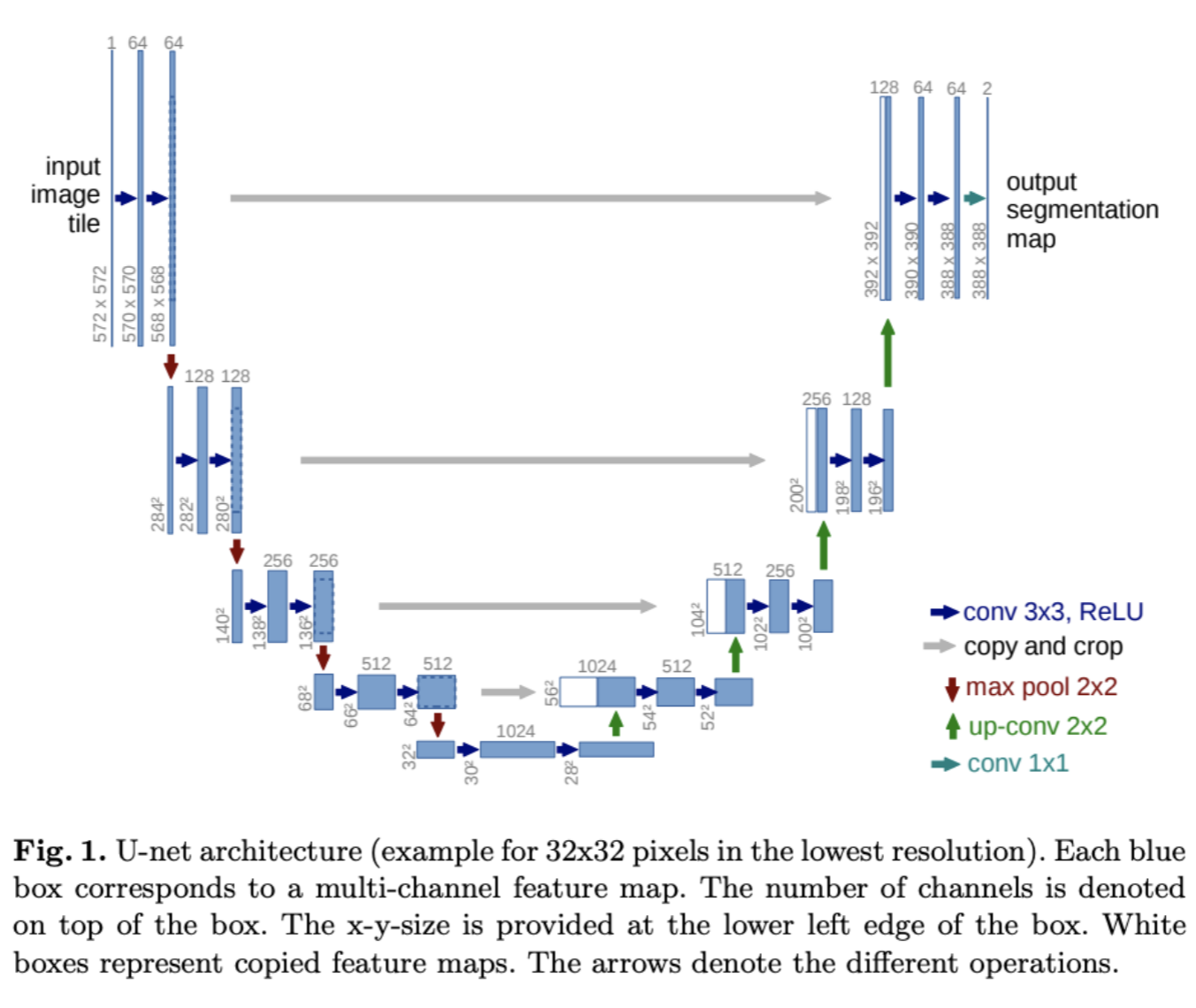
UNET: la primera arquitecura utilizada

Representación de Unet

La primera arquitectura que se utilizó con los modelos de diffusión fue la Unet, ya que es una arquitectura muy famosa en el campo de la visión por computador. Al fin y al cabo, como este primer artículo lo que generaba eran imágenes, utilizar este modelo suponía tener un muy buen punto de partida.

Pero cuando introducimos la Unet en el universo de los modelos de difusión, hay un giro interesante. No es simplemente copiar y pegar; la implementación lleva un toque especial para que todo encaje con el proceso de difusión, tal y como se puede ver en la siguiente imagen que representaría una vista desde arriba de la arquitectura del modelo:

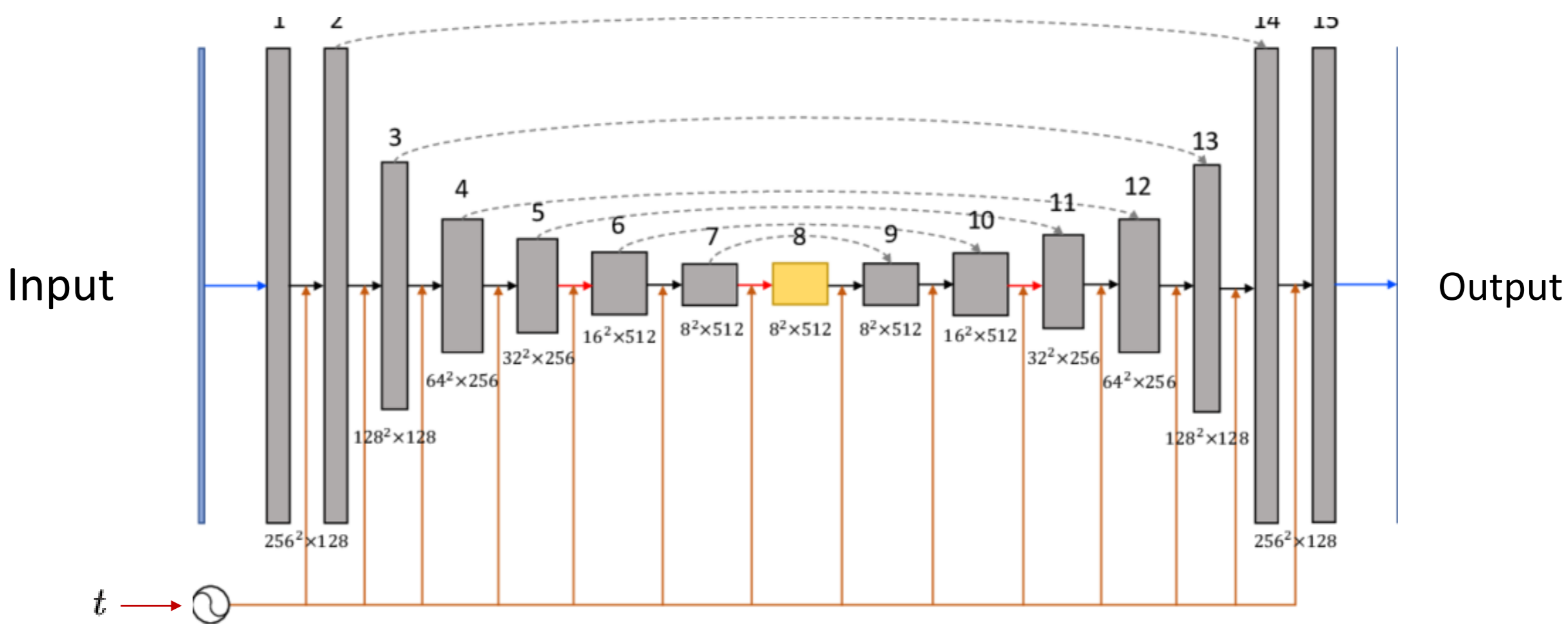Representación de Unet vista desde arriba

El valor de $t$, o el paso en la cadena de Markov, no se introduce en la red de manera directa. En cambio, se emplea una técnica inspirada en los transformers llamada positional encoding, donde $t$ se codifica a través de múltiples señales senoidales. Este método, más conocido por su uso en la arquitectura de los transformers para mantener la noción de posición en secuencias de texto, aquí se adapta para inyectar la dimensión temporal sobre el paso en el que nos encontramos en la cadena dentro de la red.

Esta codificación no solo se introduce al principio, sino que se va “recordando” a lo largo de toda la arquitectura de la Unet, asegurando que el modelo esté constantemente “consciente” del paso en el que se encuentra en el proceso de difusión. Este enfoque permite que la Unet ajuste su predicción de manera más precisa, mejorando así la calidad de la reconstrucción de las imágenes.

Consideraciones especiales

Cuando nos metemos de lleno en la implementación de modelos de difusión, hay dos cuestiones que personalmente he comprobado experimentalmente que son cruciales para el éxito:

1. Recordar constantemente la $t$ dentro del modelo: es como tener un reloj interno que ayuda al modelo a entender en qué momento del proceso de difusión se encuentra, ajustando su comportamiento en consecuencia.

2. Aplicar skip connections es vital: al igual que se aprecia en las líneas discontinuas grises de la última imagen de la Unet, recordar y reutilizar lo que se ha aprendido en capas anteriores del modelo es fundamental. Estas conexiones permiten que la información fluya directamente entre capas no consecutivas.

Sin estas dos elementos probablemente los modelos de difusión no puedan converger adecuadamente.

¿Qué viene después?

Si has seguido hasta aquí, seguro que ya tienes una buena base sobre los modelos de difusión, especialmente lo que se desgrana en el documento original. Pero como bien sabrás, el campo de la inteligencia artificial no para de evolucionar, y desde la presentación inicial de estos modelos en 2020, hemos visto avances significativos. Aquí te dejo un breve repaso de algunos trabajos importantes que han surgido, con la esperanza de poder profundizar en ellos más adelante.

Improved DDPM

Este artículo de OpenAI profundiza en el uso del Cosine Scheduler, una estrategia que degrada la información de la muestra original de manera más gradual a lo largo de la cadena de Markov. Además, resaltan los beneficios de predecir $\Sigma_\theta(x_t,t)$, un aspecto que el artículo original omitió.

CFG: Classifier-free guidance

Este enfoque propone un método para enseñar a los modelos de difusión a manejar la distribución de varias clases simultáneamente y cómo generar muestras específicas de una clase determinada, todo esto usando información condicionada. Este método no solo es innovador, sino que también mejora la calidad de las muestras generadas.

DDIM: Denosing Diffusion Implicit Models

Aunque ya se ha mencionado antes, los DDIM representan una variante interesante de los modelos de difusión. La clave de estos modelos es que, a pesar de ser entrenados de la misma manera, permiten saltar pasos en la cadena de Markov durante la generación de muestras, haciéndolos mucho más rápidos.

Fuentes recomendadas

• Artículo original de DDPM
• Artículo original de Improved DDPM
• Artículo original de CFG
• Artículo original de DDIM

En Youtube tienes estos videos que fueron clave para que puediera entenderlo todo:

Este primer video es una maravilla, en 30 minutos te explica todos los conceptos matemáticos de la difusión, probablemente la mejor fuente que he encontrado para entenderlo todo.

Este una continuación del vídeo anterior, en este implementa un modelo de difusión en Pytorch desde 0, una vez más, muy recomendable.

Finalmente, este vídeo también está muy bien, ya que lee el paper original y lo explica todo paso a paso.

Con todo esto, acabo mi explicación sobre el primer artículo que presentó los DDPM. Espero que haya sido de utilidad, y que más o menos lo haya podido explicar claramente y de forma amena. Si tienes alguna duda, o consideras que he podido cometer alguna pequeña errata, ¡te animo a que me lo pongas en comentarios!